Rowin Andruscavage
http://hairball.bumba.net/~rwa2/school/enpm642/Arcology.html
University of Maryland
ENPM 642 Spring 2003
John S. Baras ; AV Williams 2249
Abstract:
An arcology is a combination of architecture with ecology, essentially forming an environmentally friendly human living system well suited to systems engineering analysis. This document defines and describes a network queuing simulation model that might be used to perform trade study analysis on such a system. The model attempts to structurally decompose the human habitat into groups of subsystems on all scale levels that interact through the exchange of resource groups. The resulting resource flows are quantified into performance metrics used to compare different types of arcologies to current living conditions. Bottom-up scenarios of arcology models will be compared to top-down scenarios constructed based on present day statistical data. Tradeoff studies focus on feasibility of coverage based on differing transportation network topologies.
Table of Contents
GeneralClasses Object Model Diagram
System Requirements Allocation
Arcology Primitive Requirements
Primary Energy Consumption by Fuel
Optimization Problem Formulation
Preliminary System Design Solution
 System Description
System Description
The concept of the arcology was first introduced in the 1950s by architect Paolo Soleri as the ultimate urban planning solution to the problems of metropolitan growth. Continuing trends in the expansion of metropolitan areas have contributed to explosive growth of low density suburban sprawl, the decay of inner city urban areas, and finally the indiscriminate destruction of natural environments to make room for a human habitat system which is increasingly less efficient, convenient, and aesthetic. The concept of the arcology attempts to reverse those trends by providing a compact city infrastructure that works.
What is an arcology? Featured in several science fiction works as the city of the future, an arcology is more than just a structure... a "superbuilding" that contains everything you would expect to see in a current city. The arcology integrates living spaces and working spaces with transportation systems that connect it all. One of the fundamental differences is that it heavily involves the third dimension into city planning, whereas current planning is done by zoning commercial / residential / industrial in an ad hoc fashion (well, by government committee through series of votes, demonstrations, bribes, and legal means applied in a reactive manner which fulfills actual requirements just as well as ad hoc design process). Naturally, the arcology is simply what a city would be if it was to be designed by competent systems engineers (of course, a feat easier said than done).
Another advantage to designing cities from the perspective of an arcology is that it forces you to take all scale levels into account in the design. This allows the arcology to transition better as new technologies are put into place.
On the national level, arcologies would be constructed to connect well to other arcologies, with effective transportation and distribution systems. Current cities have transportation problems. Many cities grew around ports. However, shipping is no longer the primary means for distributing goods. The United States has invested heavily in the highway system. However, around many cities these get tied up in rush hour congestion, resulting in delays and waste. Airports are usually built too far from the city to connect well to mass transit systems, or have been enveloped (and throttled) by the city and create a nuisance to nearby residents.
 On
the personal level, much infrastructure for living does not have flexibility
for change. We are still using much of the same infrastructure developed over a
century ago for power and telephone. Additional systems have sprouted up on top
of these networks, such as cable television and various wireless networks that
compete for spectrum, and a myriad of PBX, fiber optics, etc. for corporations.
Various combinations of water mains, sewage systems, natural gas pipelines. A
modular arcology structure would need to be able to adapt to support new
networks.
On
the personal level, much infrastructure for living does not have flexibility
for change. We are still using much of the same infrastructure developed over a
century ago for power and telephone. Additional systems have sprouted up on top
of these networks, such as cable television and various wireless networks that
compete for spectrum, and a myriad of PBX, fiber optics, etc. for corporations.
Various combinations of water mains, sewage systems, natural gas pipelines. A
modular arcology structure would need to be able to adapt to support new
networks.
The purpose of an arcology is to create a compact, organized structure for people to live and work. It should be designed to improve and maximize upon the quality of life of its residents, while also performing well economically, in production, and in development. The transportation system is one of the keys to making the system perform. This connective tissue accounts for how well most of the rest of the system can perform.
Paolo Soleri describes several arcology designs that could be used to replace major cities or serve well in several environmental settings. This project would create a tool that could be used to quantitatively analyze the benefits of replacing cities with arcologies. This report describes the systems engineering of a tool to perform systems engineering preliminary design & benefits analysis.
Previous well-known works that tackle this task includes two
open-ended games from Maxis (now part of Electronic Arts) that approach the
problem from two different scales:
SimCity and The Sims. Beyond that, there is not much published in the way of city
and lifestyle simulation. This is
probably partly because most of this analysis can be done more simply using
historical data tracked by government statistical agencies, and because most of
the simulation writers are more busy simulating more interesting things such as
data and transportation networks.
Not many people are in a position to design cities, however, almost
everyone needs to work within the infrastructure of one, so it would be  worthwhile
to create a model if only to serve as a dynamic demand generator used to plug
input parameters into these data and transportation networks. Surely they can use historical data as
inputs, but this breaks down when a system they are designing may have a
significant effect on the input data.
worthwhile
to create a model if only to serve as a dynamic demand generator used to plug
input parameters into these data and transportation networks. Surely they can use historical data as
inputs, but this breaks down when a system they are designing may have a
significant effect on the input data.
One item of study that this type of simulation makes feasible is the relationship between these data networks and transportation networks. For example, if a city decides to spend money upgrading their data infrastructure so more people might be able to telecommute to work, this may have a noticeable impact on the load on their mass transit system. This simulation could aid as a decision-making support tool that could actually tie the network and transportation models together.



Above: Arcologies from SimCity 2000
Insets: Concept art of arcologies in SimCity 3000
The approach for this project involved using Ilogix Rhapsody® in C++ Development Edition to construct UML diagrams of the system. Work proceeds under the expectation that the code generation facilities of Rhapsody could be used to embed C++ source code in the framework to compile and run a working executable as part of the Systems Modeling and Analysis course in the future. As an added benefit, Rhapsody also provides documentation generation of the model in rich text format. This project documentation is interspersed into this report with appropriate commentary and then exported to html.
One of the side effects of using Rhapsody include some subtle differences in naming conventions, presumably used to simplify the merging of the standard OMG UML specification with the practical realities of software engineering frameworks. Notably, Rhapsody uses "Object Model Diagrams" in place of both "Class Diagrams" and "Instance Diagrams". Since this project deals with abstract models, we will almost always be referring to class diagrams except when dealing with actual scenarios.
System Model
Concept Requirements
Goals
One of the characteristics of systems such as cities that grew by evolution rather than by design is that they lack fundamental policies that drive their design. Components of the city usually come about in a reactionary manner: fire protection services are built after too many buildings burn down, airports are built to serve cities after they have already grown too dense to accommodate one in a central location, tap water distribution systems are gutted out and replaced only after the old ones were too heavily loaded to be sanitary.
Hindsight being 20/20, it is worthwhile to dwell on past mistakes and develop urban planning with a systems engineering process worthy of supporting a megalopolis. The first step is to develop a set of goals and objectives that drive the design of the city. At first glance, the goal of a city (at least as envisioned in SimCity) ought to be to grow and prosper. However, this overlooks the city’s primary responsibility to fulfill the needs and look after the well being of its inhabitants. For that, we can look at it from an individual level on par with the scale of The Sims:
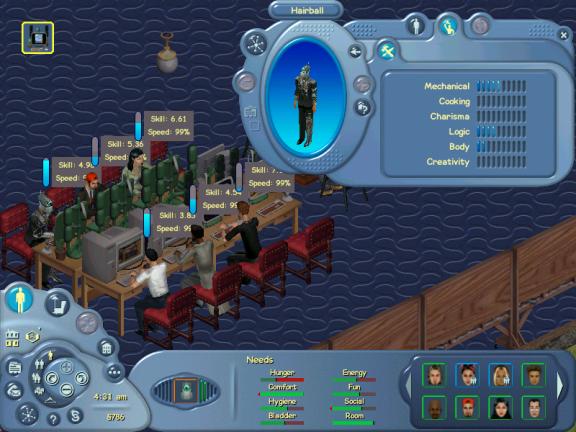
The Sims offers 8 needs for each of their simulated characters: Hunger, Energy, Comfort, Fun, Hygiene, Social, Bladder, and Room
This model takes an even simpler approach:
- Shelter – where people live and sleep (accounts for Energy, Comfort, and Room)
- Food / Air / Water – the raw materials people need to consume to live, or at least not starve to death (accounts for Hunger)
- Health – maintenance factors, such as cleanliness, waste, (accounts for Hygiene and Bladder)
- Work – most people need something productive to do when they aren’t attending to their other needs. This could take the form of working for money, or being educated to increase their knowledge bank of information.
- Entertainment – if people aren’t doing something productive, they’re probably doing something fun to while away their time (accounts for Fun and Social)
In order to fulfill these needs for all of the city’s inhabitants efficiently, what they are really looking at is developing infrastructure to move resources around so that each of these needs can be catered to. This simulation model takes on abstract views of these resources and the transportation networks that move them around.
Objectives
So what should our objectives be, if we are to meet our goals, how can we form an objective function for optimization? Of course, we’re talking about multivariate optimization of multiple goals.
- Continually improve the quality of life for inhabitants
- Accelerate development of improvements to the body of knowledge
- Maximize productivity, performance.
- Optimize resource consumption to achieve balance with the environment.
- Avoid optimizing the whole at the expense of the few by trampling individual freedoms. Add structure to the system by providing opportunities and alternatives, not imposing restrictions.
In order for the simulation model to be effective, it should be capable of assigning metrics corresponding to these objectives, and computing them based on the simulation inputs. The simulation inputs and execution will have to sufficiently model real life enough to be able to produce a valid estimate of these performance metrics.
Use Case Diagrams
As
described, the arcology use cases are simple enough, and represent a few
different modes of operation. The
system boundary is provided by the living quarters, which, contrary to its
name, extends beyond the individual's residence and just encompasses all the
locations where they go about their business. The arcology simulation model will need to be flexible
enough to model these types of activities in order to be used for design.
Live
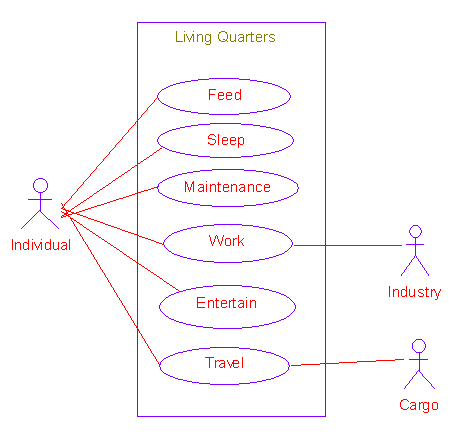
The one
new activity introduced by this diagram is the Travel interaction. As mentioned, not all of these use
cases occur in one location, so the Travel case takes care of moving the
individual from one location to another.
This interaction is performed through one of the Cargo Transportation
Infrastructure classes, which will be detailed in the System Structure.
Actors:
Individual
An inhabitant of the system.
Relations:
itsFeed
Association with Feed, Multiplicity of 1,
Bi-directional
itsSleep
Association with Sleep, Multiplicity of 1,
Bi-directional
itsMaintenance
Association with Maintenance, Multiplicity of 1,
Bi-directional
itsWork
Association with Work, Multiplicity of 1,
Bi-directional
itsEntertain
Association with Entertain, Multiplicity of 1,
Bi-directional
itsTravel
Association with Travel, Multiplicity of 1,
Bi-directional
Industry Entity
by which the individual is employed.
Relations:
itsWork
Association with Work, Multiplicity of 1,
Bi-directional
Cargo
Transportation
Infrastructure responsible for moving people around (as well as resources).
Relations:
itsTravel
Association with Travel, Multiplicity of 1,
Bi-directional
Use Cases:
Sleep
Everyone
needs a place to rest for a significant portion of the daily cycle.
Relations:
itsIndividual
Feed
Consumption
of food and water resources.
Relations:
itsIndividual
Maintenance
Miscellaneous
cleaning tasks, such as bathing, brushing teeth, doing laundry, dishes, etc.
would be represented here.
Relations:
itsIndividual
Work
Work is
a transaction between and individual and an industry to exchange money for
productivity. In this case,
productivity fuels the reactions that the industry performs.
Relations:
itsIndividual
itsIndustry
Entertain
Entertainment
can take on several forms, from merely socializing with other individuals,
engaging in solitary entertainment interactions (TV, games), to mass
entertainment (theatre, etc.).
Extension
points:
Social
Relations:
itsIndividual
Travel
An
individual is able to travel through the transportation infrastructure to
commute to work or to travel to places to fulfill their other needs, such as
for food or social interaction with friends.
Relations:
itsIndividual
itsCargo
Use cases for the simulation model:
- Set up a modeling scenario using input data.
- Build bottom-up scenario: Since the arcology is designed from the ground-up, starting at the individual level, the structure of our model would allows us to calculate the aggregate performance at higher levels of organization, such as a the city and national level.
- Define # of simulation units, connectivity between units, schedule of transaction events, schedule of reaction events, initial conditions.
- Output aggregate performance for groups of units.
- Build top-down scenario: The present day scenario is built in a top-down fashion from various government data sources. Statistics are only tracked from relatively high levels on the organizational hierarchy, so we must extrapolate some data to flow down to fill the detailed subcells of the structure.
- Define high-level consumption rates for groups (using publicly tracked & available data), provide distribution histograms for each type of resource & transaction rates for each subunit.
- Output unit-level quality of life, performance.
- Execution of simulation model to produce output data.
- Postprocessing & analysis of output data into performance metrics.
- Design-of-Experiments method of parametric analysis for solution space exploration & optimization.
System Structure
Rhapsody can organize things into collections called packages, which roughly correspond to namespaces in C++. This allows elements to be sorted and separated cleanly.
The basic model consists of an overall package named GeneralHabitat, which contains base classes and three more packages to organize resources, reactions, and transportation methods.
GeneralHabitat Package
Generalized
resource queuing and transportation model of living support systems.
A
scenario is required to build up a model of a system by creating a hierarchy of
cells that connect to each other via transportation network
infrastructures. These cells then
begin to perform resource transactions between each other and resource
reactions within themselves to simulate the daily operations of the system and
observe it from different levels of detail, scaling from the individual to the
city to the world. The transaction
approach is well suited for implementation in a discrete event simulation.
Much of
the model is static, such as monetary costs for resources or the structure of
cells. This model is not intended
to perform dynamic economic simulations or find ecological balances between the
deaths and birth rates of people or towns; those functions have been well
studied. (That said, the nature of
the event-driven simulation framework makes it easy to patch in such
functionality by manipulating variables or cleverly reorganizing the scenario
outside of the simulation.)
Instead,
this model is merely intended to construct an overglorified spreadsheet used to
perform preliminary design and calculate rough benefits analysis on changes to
ways of life, quantifying answers to such questions as: "how much energy
might a city save if everyone installed more efficient light bulbs?" or
"how much time can we save if we staggered a city's work schedule to
relieve rush hour congestion?"
The GeneralClasses object model diagram
(Rhapsody's internal name for a UML class diagram) depicts the base simulation
classes and generally encompasses the entire design of the simulation. All object model diagrams following
this would actually constitute scenario-specific use cases that highlight the
use of the base simulation classes.
GeneralClasses Object Model Diagram
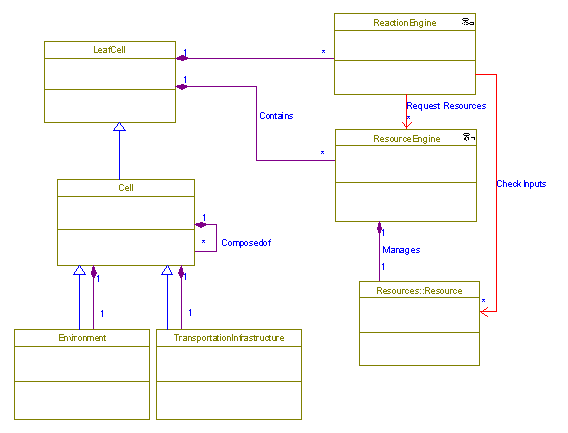
Nested
Packages:
Resources
CellHierarchy
Transportation
Reactions
Cell
The
fundamental unit of structure.
Each cell represents an identifiable entity, which contains its own
collection of resources. These
resources can be traded with other cells, or undergo reactions within the cell
to transform groups of resources into other types of resources.
Generally,
there are five basic types of cells that work together: The entity itself, the
entity's environment, the entity's transportation infrastructure, and leaf
cells to represent individuals and industries.
To
further complicate matters, entities are arranged into hierarchies of
subcells. This allows us to view
the system on several levels of detail, from global down to the individual. To do this, we introduce the constraint
that a cell's resources always equals the sum of the resources of all of its
child subcells.
Relations:
itsSubCell
Each branch cell may contain
several subcells
Composedof
Composition of Cell, Multiplicity of *, Bi-directional
itsCell
Composedof
Association with Cell, Multiplicity of 1,
Bi-directional
itsEnvironment
Composition of Environment, Multiplicity of 1,
Bi-directional
itsTransportationInfrastructure
Composition of TransportationInfrastructure,
Multiplicity of 1, Bi-directional
Superclasses:
LeafCell
Public
Subclasses:
City
Community
Environment
Household
Nation
Region
TransportationInfrastructure
World
LeafCell
Leaf
cells are a special type of cell reserved for individuals and industries. These cannot be subdivided further into
subcells, and thus lack an environment or a transportation infrastructure to
support those subcells.
Relations:
itsResourceEngine
Contains
Composition of ResourceEngine, Multiplicity of *,
Bi-directional
itsReactionEngine
Composition of ReactionEngine, Multiplicity of *, Bi-directional
Subclasses:
Cell
Individual
Industry
CellHierarchy
Object Model Diagrams:
We model the area of interest by breaking it down into a hierarchy of cells and subcells that work at a different level of detail. There are essentially two types of units, parent nodes and leaf nodes, with the only distinction being that leaf nodes do not have any subcells. One possible scheme for defining this hierarchy is presented in the CellTypes class diagram. It's important that all of the subcells add up exactly to form the parent cell, so in some cases, it would be necessary to define subcells that represent everything that might be left over after allocation into existing subcells. For example, the rural areas not part of a city would be lumped into a special residual "City" subcell to be included as part of a "Nation". Similarly, homeless people and vagrants would be lumped together into a special "Household" or "Community" subcell to be included as part of "City" data. This should be an acceptable practice, since these units may tend have similar characteristics.
CellTypes
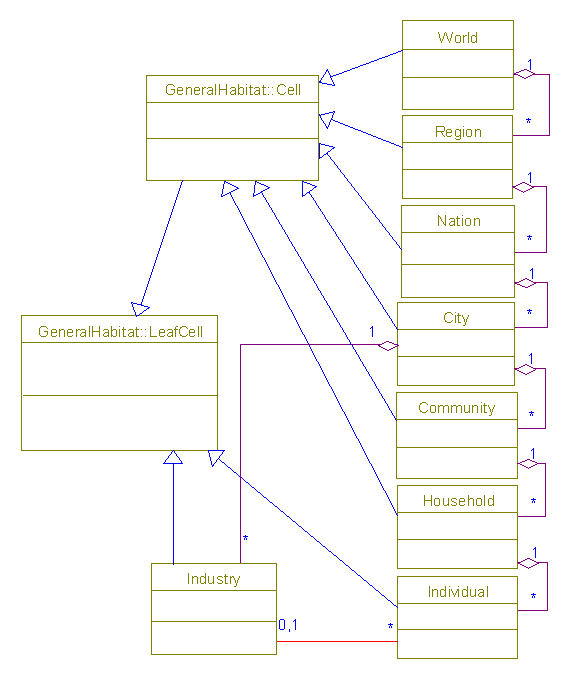
Classes:
World
The
limits of the size of the system.
Of course, the architecture of the model is left open to envelop
interplanetary commerce between worlds in the distant future.
Relations:
itsRegion_1
Aggregation (me as the whole part) of Region,
Multiplicity of *, Bi-directional
Superclasses:
Cell
Public
Region
A
geographic region would tend to be composed of several nations with a common
situation. Of course, large
nations may exist over several regions.
For our purposes, we'll simplify by assuming all nations are smaller
than the regions they are in.
Relations:
itsWorld_1
Association with World, Multiplicity of 1,
Bi-directional
itsNation
Aggregation (me as the whole part) of Nation,
Multiplicity of *, Bi-directional
Superclasses:
Cell
Public
Nation
A nation
sets the policy for international trade and commerce. Plus, data is often available on the national level for
input into the top-down models.
Relations:
itsRegion
Association with Region, Multiplicity of 1,
Bi-directional
itsCity
Aggregation (me as the whole part) of City,
Multiplicity of *, Bi-directional
Superclasses:
Cell
Public
City
A city
would be the highest level of organization represented by an individual
arcology. Several cities would be
interconnected to form a nation.
One "city" cell unit can be put aside to account for all rural
areas not included in other cities.
Relations:
itsNation
Association with Nation, Multiplicity of 1,
Bi-directional
itsCommunity
Aggregation (me as the whole part) of Community,
Multiplicity of *, Bi-directional
itsIndustry
Aggregation (me as the whole part) of Industry,
Multiplicity of *, Bi-directional
Superclasses:
Cell
Public
Community
Families
tend to cluster into communities, which in turn form cities.
Relations:
itsCity
Association with City, Multiplicity of 1,
Bi-directional
itsHousehold
Aggregation (me as the whole part) of Household,
Multiplicity of *, Bi-directional
Superclasses:
Cell
Public
Household
A
household would consist of a family of several individuals living together in
one residence.
A family
doesn't necessarily include extended family, or preclude the existence of other
arrangements such as roommates.
Relations:
itsCommunity
Association with Community, Multiplicity of 1,
Bi-directional
itsIndividual
Aggregation (me as the whole part) of Individual,
Multiplicity of *, Bi-directional
Superclasses:
Cell
Public
Individual
A leaf
node in the hierarchy, the Individual cannot be broken down into any more
subcomponents (we can only hope).
Most individuals will also work for an industry.
Individuals
are free to move from place to place as part of their daily lives. This allows them to commute to work or
to visit friends in another household and transfer their resource consumption
to stress the infrastructure at other locations.
When
individuals travel, it puts a strain on the transportation infrastructure.
Relations:
itsHousehold
Association with Household, Multiplicity of 1,
Bi-directional
itsIndustry
Association with Industry, Multiplicity of 0,1,
Bi-directional
Superclasses:
LeafCell
Public
Industry
Cities
have a special type of leaf node called Industry, which essentially employ
several Individual units to perform certain specialized reactions on particular
resources in bulk. Generally, they
consume energy resources to refine material resources.
Relations:
itsCity
Association with City, Multiplicity of 1,
Bi-directional
itsIndividual
Association with Individual, Multiplicity of *,
Bi-directional
Superclasses:
LeafCell
Public
Environment
A
special passive cell that will always yield any resources that it has and
accept any waste that is ejected into it.
Instead of interacting with other cells on the same level, it only
interacts with subcells. So, for
example, a nation's resources can be split amongst its cities, and city level
waste gets deposited in the nation's environment (as opposed to some other
nation's environment).
Relations:
itsCell
Association with Cell, Multiplicity of 1,
Bi-directional
Superclasses:
Cell
Public
TransportationInfrastructure
A
special cell that interacts with subcells. It represents the connective tissue that allows resources to
transit between subcells, and it takes both money and fuel in the process. Several types of transportation
infrastructures can be defined with different characteristics in terms of
resource burn rates.
Relations:
itsCell
Association with Cell, Multiplicity of 1, Bi-directional
Superclasses:
Cell
Public
Subclasses:
Cargo
Pipeline
Radio
Wire
Attributes:
Maintenance
Monetary maintenance cost incurred
to keep this system up and running per unit cycle.
Type of double, Public
TransitCost
Monetary cost required to move a
unit of resource through this transportation infrastructure per unit distance.
Type of double, Public
Value
Infrastructure build value, how
much money needs to be invested to put this transportation infrastructure in
place so it can be used.
Type of double, Public
Transportation
The transportation network serves as connective
tissue that joins the nodes of the structure together. It is up to the scenario to define the
connectivity graph, but once accomplished this will compute the overhead in terms
of resource burn to transfer individuals and cargo through the network.
Object Model Diagrams:
ConnectiveTissue
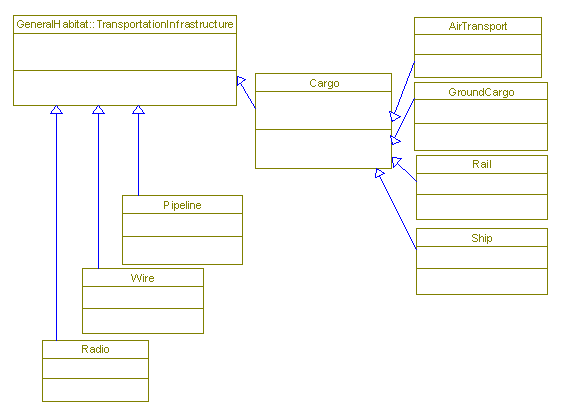
Classes:
Cargo
A
generalized form of transportation for passengers and cargo. Only these forms of transportation can
handle material goods and individuals.
Superclasses:
TransportationInfrastructure
Public
Subclasses:
AirTransport
GroundCargo
Rail
Ship
Attributes:
NetworkCapacity
The number of transport units the
transportation infrastructure can handle.
As network capacity approaches this number, congestion effects set in.
Type of int, Public
numUnits
Number of transport units actively
using the system at any given time.
When this number nears the NetworkCapacity, congestion delays set in
which begin to cut into the efficiency of the system.
Type of int, Public
AirTransport
Expensive but fast, and often must be used in a multimodal fashion, where households must transfer their wares up to the city level first before making airhops between cities.
Superclasses:
Cargo
Public
GroundCargo
Well connected, reaching every location with road coverage.
Superclasses:
Cargo
Public
Rail
High initial infrastructure costs and not very well connected, but fairly economical once everything is in place.
Superclasses:
Cargo
Public
Ship
Only a boon to certain cities, and requires some contention for port infrastructure.
Superclasses:
Cargo
Public
Pipeline
Pipeline
infrastructure is good for transporting fluid commodities, such as water,
natural gas, sewage, etc.
Superclasses:
TransportationInfrastructure
Public
Wire
Distribution
system for electricity and information
Superclasses:
TransportationInfrastructure
Public
Radio
Distribution
system for information
Superclasses:
TransportationInfrastructure
Public
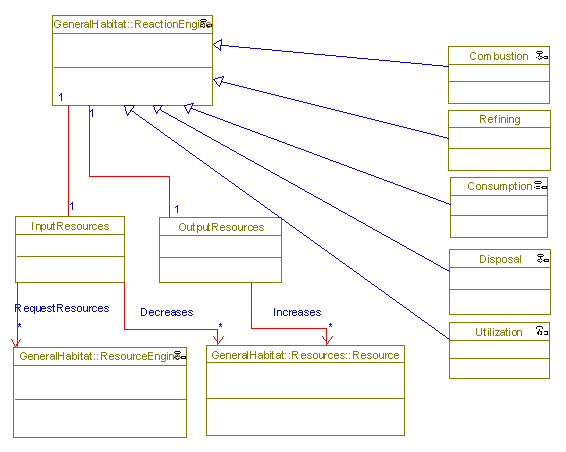
Reactions
This package defines reactions that can occur
within cells to transform one set of resources into another set of
resources. The definition of the
reaction governs changes to the quantities of inputs and outputs, and balances
them the same way a chemical reaction would be balanced.
Object Model Diagrams:
ReactionTypes
The icons in the top right of some of the classes indicate that those classes have activity diagrams associated with them. These diagrams can be viewed in the corresponding System Behavior section. The specific reactions on the right inherit the activity diagrams from parent classes, where they can be extended. The "Refining" class appears to have "lost" its activity diagram, though, probably due to a bug in the way Rhapsody inherits statecharts; it should be possible to fix by deleting the class and recreating it.
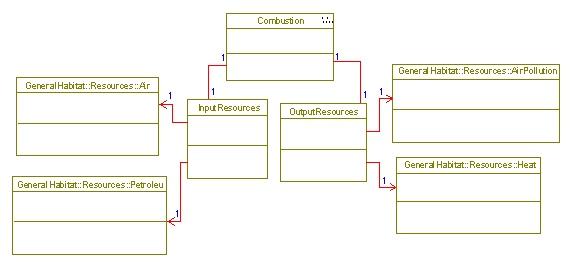
CombustionReaction
This diagram highlights one of the reactions in
detail. Other reaction types would
look very similar to this diagram with different combinations of input and
output resources.
Resources
This package details the various
generalizations of resources available in the model.
Object Model Diagrams:
Resource
A
particular resource of interest that can be contained, traded, or reacted
within cells.
Relations:
itsResourceEngine
Manages
Association with ResourceEngine, Multiplicity of 1,
Bi-directional
Subclasses:
Fuel
Information
Money
Waste
Attributes:
Qty
Type of double, Public
Unit
Type of OMString, Public
ResourcesTypes
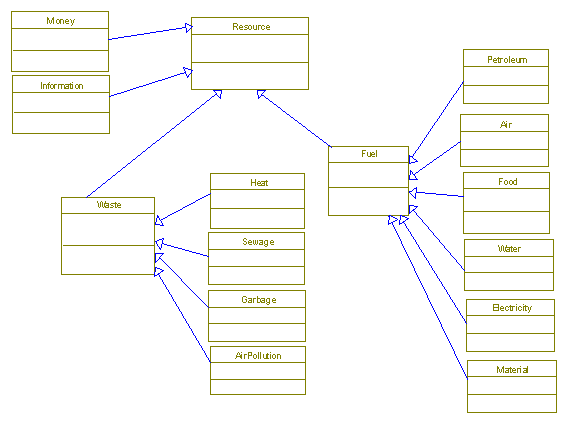
Money
Financial resources are often exchanged for goods and services, so it's worth tracking how much each cell has on reserve.
Superclasses:
Resource
Public
Information
Information can also be transferred and accounts for education activities or entertainment.
Superclasses:
Resource
Public
Fuel
The Fuel superclass generally refers to any resource that is useful.
Superclasses:
Resource
Public
Subclasses:
Air
Electricity
Food
Material
Petroleum
Water
Air
Rather than get too specific in chemistry terms, this class represents clean useful air for breathing or to provide oxygen for combustion.
Superclasses:
Fuel
Public
Electricity
Electrical distribution is one of the oldest networks in the world and serves as a catalyst for many other useful reactions, or merely as a utility to improve the quality of life.
Superclasses:
Fuel
Public
Food
Anything people can eat.
Superclasses:
Fuel
Public
Material
Any kind of object or artifact that might be transferred. Along with the mass value inherited from resource, material can also have a value density, which can increase with the refinement reaction to represent a lot of what industry does.
Superclasses:
Fuel
Public
Petroleum
More traditional fuel products that are not necessarily restricted to oil or derivatives. Anythings that burns to produce energy could be included, such as coal and wood.
Superclasses:
Fuel
Public
Water
Clean potable water for drinking or for maintenance.
Superclasses:
Fuel
Public
Waste
Superclass that represents byproducts that cells probably don't want to keep around, but that need to be tracked and disposed of appropriately. Waste can still put a load on the transportation infrastructure, and require industrial resources to treat and refine properly.
Superclasses:
Resource
Public
Subclasses:
AirPollution
Garbage
Heat
Sewage
AirPollution
Any kind of gaseous waste.
Superclasses:
Waste
Public
Garbage
Solid waste products, mostly discarded materials.
Superclasses:
Waste
Public
Heat
Otherwise known as entropy, almost every process surely creates waste heat that needs to be dissipated.
Superclasses:
Waste
Public
Sewage
Liquid waste that might be drained through the sewage system.
Superclasses:
Waste
Public
System Behavior
The simulation model is based on a discrete event simulation engine. This means that state changes in the system structure are triggered by the firing of events which occur along the global time line queue. The model executes by populating the global time queue with scheduled events and firing those events in order. Every time an event is activiated, the system global time is advanced to that time. Any state transitions in the model that were blocking on this event are executed so they can perform their activities, which often result in the scheduling of more events in the future. Thus the simulation perpetuates events and continues in time until there are no more events left on the simulation queue.
Events:
evFeed
Event
signalling that the person should make an attempt at going somewhere to eat.
evSleep
Event
signalling person to go somewhere (preferably home) so they can sleep.
evWakeup
Event
signalling a person to wake up and begin their day.
Individual
The individual transitions from state to state in their daily activities triggered by these events. A fairly simple schedule could be arranged as follows to implement a statechart representing a typical person's day. The statechart depends on having the right combination of events defined and triggered to advance the individual through the full daily cycle.
Statechart
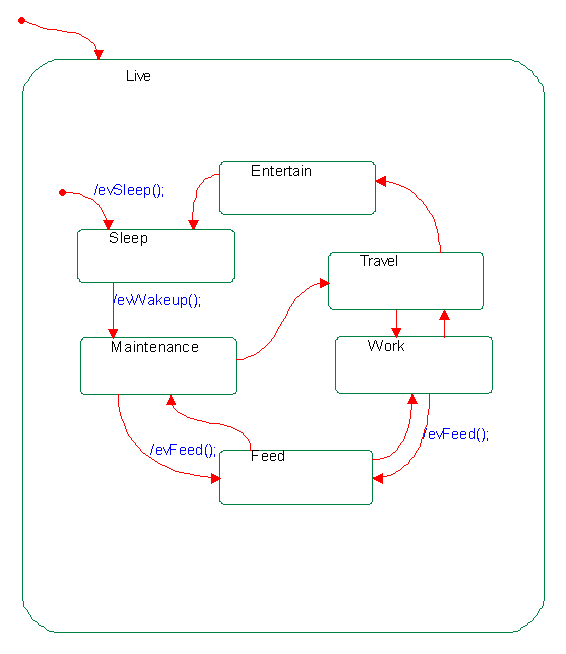
ROOT
Or-state
Substates:
Live
Default Transition
Target:
Live
Live
Or-state
Substates:
Entertain
Feed
Maintenance
Sleep
Travel
Work
Default Transition
/evSleep();
Target:
Sleep
Entertain
Or-state
Out Transition
Target:
Sleep
Feed
Or-state
Out Transition
Target:
Maintenance
Out Transition
Target:
Work
Maintenance
Or-state
Out Transition
/evFeed();
Target:
Feed
Out Transition
Target:
Travel
Sleep
Or-state
Out Transition
/evWakeup();
Target:
Maintenance
Travel
Or-state
Out Transition
Target:
Work
Out Transition
Target:
Entertain
Work
Or-state
Out Transition
/evFeed();
Target:
Feed
Out Transition
Target:
Travel
ResourceEngine
Each
resource engine keeps track of the flow of one resource within a cell. This includes the input of resource
from the environment, trade of resources with other cells, internal reactions
that transform resources to and from other resources, and waste resource output
back to the environment.
The
resource engines are initialized to fire push/pull transaction events at
regular intervals. Pull
transactions would offer to exchange monetary resources for goods and services
such as food or electricity. Push
transactions relate to the expulsion of waste, and would end up in the
immediate environment unless picked up by a transportation system to take to,
say, a waste processing plant (represented by an industry) first.
Relations:
itsResource
Each ResourceEngine manages the quantity
of one resource for each Cell unit through transactions in/out of the
environment, trade with other Cell units via connective transportation cells,
or internal reactions within a Cell.
Manages
Composition of Resource, Multiplicity of 1, Bi-directional
itsLeafCell
Contains
Association with LeafCell, Multiplicity of 1,
Bi-directional
Attributes:
Amount
Amount of resource requested per
cycle
Type of double, Public
Interval
Time interval between requests
Type of double, Public
Activity Diagram
Resources essentially attempt three types of transactions:
1. A request for resources from its parent cell or environment, in client/server pattern.
2. A peer-to-peer trading agreement scheduled through the scenario setup.
3. A dump of resources back to its parent cell or environment.
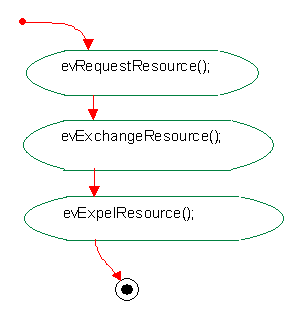
ROOT
Or-state
Substates:
Expel
Pull
state_3
Trade
Default Transition
Target:
Pull
Expel
Push transaction to deposit waste
into the waste management infrastructure (or the environment).
Action State
EntryAction
evExpelResource();
Out Transition
Target:
state_3
Pull
During initial scenario setup, set
a starting
Action State
EntryAction
evRequestResource();
Out Transition
Target:
Trade
state_3
Local Termination State
Trade
Transaction to exchange resource
with another cell on the same level.
Action State
EntryAction
evExchangeResource();
Out Transition
Target:
Expel
ReactionEngine
Resources
are required to fuel several reactions that occur within a cell. These reactions are driven by the reactionengines
associated with a cell to consume several resources and turn them into other
resources and waste.
When
enough of the input resources become available, the reaction event can
commence. Otherwise, the reaction
engine asks the resource engine to request the required resources through pull
transactions.
Several
reaction types are available, but the assigment and scheduling of reaction
events is up to the scenario builder.
Relations:
itsLeafCell
Association with LeafCell, Multiplicity of 1, Bi-directional
itsResourceEngine
Request Resources
Association with ResourceEngine, Multiplicity of *,
Uni-directional
itsResource
Check Inputs
Association with Resource, Multiplicity of *,
Uni-directional
itsInputResources
Association with InputResources, Multiplicity of 1,
Bi-directional
itsOutputResources
Association with OutputResources, Multiplicity of 1,
Bi-directional
Subclasses:
Combustion
Consumption
Disposal
Refining
Utilization
Activity Diagram
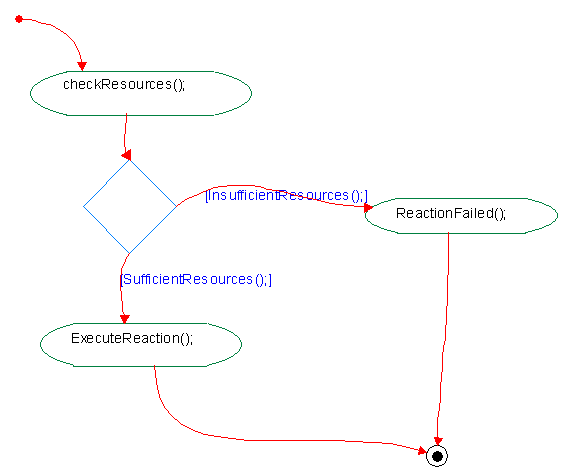
ROOT
Or-state
Substates:
state_0
state_1
state_2
state_3
Default Transition
Target:
state_0
state_0
Poll input resources to see if
there are enough raw materials ready to undergo the reaction.
Action State
EntryAction
checkResources();
Out Transition
Condition Connector
Branches:
[SufficientResources();]
Target:
state_2
[InsufficientResources();]
Target:
state_1
state_1
Record an appropriate penalty for a
failed reaction. If no penalty
action is defined, then the failure is merely recorded. These failures could then lead to a
detraction in the quality of life output metric.
Action State
EntryAction
ReactionFailed();
Out Transition
Target:
state_3
state_2
Reduce input quantities and
increase output quantities in the ratio defined in this reaction.
Action State
EntryAction
ExecuteReaction();
Out Transition
Target:
state_3
state_3
Local Termination State
InputResources
Proxy to
ReactionEngine that requests or collects resources available within the cell.
Relations:
itsReactionEngine
Association with ReactionEngine, Multiplicity of 1,
Bi-directional
itsResource
Decreases
Association with Resource, Multiplicity of *,
Uni-directional
itsResourceEngine
RequestResources
Association with ResourceEngine, Multiplicity of *,
Uni-directional
itsCombustion
Association with Combustion, Multiplicity of 1,
Bi-directional
itsAir
Association with Air, Multiplicity of 1,
Uni-directional
itsPetroleum
Association with Petroleum, Multiplicity of 1,
Uni-directional
OutputResources
Proxy to
ResourceEngine that increases associated output resources upon successful
reactions.
Relations:
itsReactionEngine
Association with ReactionEngine, Multiplicity of 1,
Bi-directional
itsResource
Increases
Association with Resource, Multiplicity of *,
Uni-directional
itsCombustion
Association with Combustion, Multiplicity of 1,
Bi-directional
itsAirPollution
Association with AirPollution, Multiplicity of 1,
Uni-directional
itsHeat
Association with Heat, Multiplicity of 1,
Uni-directional
Combustion
Reaction
in which air and petroleum fuel combine to produce waste gas (air pollution)
and heat. Often a catalyst for
operating the various forms of cargo transportation.
Relations:
itsInputResources_1
Association with InputResources, Multiplicity of 1,
Uni-directional
itsInputResources_2
Association with InputResources, Multiplicity of 1,
Bi-directional
itsOutputResources_1
Association with OutputResources, Multiplicity of 1,
Bi-directional
Superclasses:
ReactionEngine
Public
Activity Diagram
The activity diagram for Combustion is grey to indicate that it was inherited from a parent class. Any changes to the inherited activity diagram would have shown up in color.

ROOT
Or-state
Inherited
Substates:
state_0
state_1
state_2
state_4
Default Transition
Inherited
Target:
state_0
state_0
Action State
Inherited
EntryAction
checkResources();
Out Transition
Inherited
Condition Connector
Branches:
[SufficientResources();]
Target:
state_2
[InsufficientResources();]
Target:
state_1
state_1
Action State
Inherited
EntryAction
ReactionFailed();
Out Transition
Inherited
Target:
state_4
state_2
Action State
Inherited
EntryAction
ExecuteReaction();
Out Transition
Inherited
Target:
state_4
state_4
Local Termination State
Refining
Process
taking in materials and energy as input and outputting refined, higher quality
material.
Superclasses:
ReactionEngine
Public
Reaction
diagrams for Refining and the rest of the reactions would look similar to
combustion, with different combinations of resources connected to the Input and
Output classes.
System Requirements Allocation
Requirements
As with everything else in this design document, a distinction must be made between requirements for the arcology and requirements specific to the arcology simulation model (the actual system of interest). The ability for the simulation to successfully model the fulfillment of fundamental arcology requirements is in itself a requirement.
The simulation tool should be able to quantify estimates for real life occurrences. One of the odd requirements for this system is to provide special failure cases in the event that all of an individual's use cases cannot be met. While the consequences for failure to fulfill a need (such as starvation, homelessness, or sickness do to poor hygiene – all very real-world problems) does not necessarily have to be simulated to achieve its purpose in the system, failures do need to be noted and become part of the output of the system. It is of interest to note that failure is an option, and must be properly accounted for as part of the normal operation of the system.
Arcology Primitive Requirements
1. Attend to basic occupant needs defined in the Individual use cases described in Live.
1.1. Provisions (Feed)
1.1.1. Food
1.1.2. Water
1.1.3. Other consumables (vitamins, nutrients, etc.)
1.2. Indirect assets & qualities
1.2.1. Shelter, security (Sleep)
1.2.2. Health, hygiene maintenance not covered by 1.1.3 (Maintenance)
1.2.2.1. Waste removal
2. Self-sufficiency & sustainability (Work)
2.1. Extract required resources from environment
2.2. Extract labor from occupants
3. Improve quality of life for occupants (Entertain)
3.3. Social interaction
Arcology Derived Requirements
1. Transformations of resources
1.1. Fuel to Waste - byproducts of Arcology Requirements 1
1.2. Construction / deconstruction mechanism - resulting from 2.2
2. Accounting & transportation mechanism for resources
2.1. Solid - Arcology Requirements 1.1
2.2. Liquid - Arcology Requirements 1.1
2.3. Gaseous - Arcology Requirements 1.1
2.4. Information - Arcology Requirements 3.1,3.2
2.5. Monetary credits - intermediary between exchanges and transformations.
3. Transportation mechanism for resources & occupants in order to satisfy all of the above (Travel)
Simulation Requirements
1. Insert scenarios as inputs
1.1. Numbers of units involved (people, transportation mechanisms, industrial entities, etc.)
1.2. Available resources from environment, initial conditions
1.3. Resource conversion rates, schedules, functions
2. Simulation execution - model resource consumption/production rates, providing estimates on actual performance (pending validation of model)
3. Output metrics defined and calculated
3.1. Qualitative measures of performance
3.2. Quantative measures of performance
3.3. Allow possibility for formulating optimization problems to aid in benefits analysis & decision-making in arcology design.
4. Significant events (to be defined by modeling use case scenario case studies) should be modelable by scenario architecture – important activities that have impact on performance measures should not be ignored. Should provide at least approximate methods of simulating effects that are difficult to model.
5. Specification of accuracy in estimates & predictions. (Goal of ~20%)
Requirements Traceability
Feed
Sleep
Maintenance
Work
Entertain
Travel
The simulation system is capable of supporting both present day and arcology scenarios. We'll perform a traceability exercise by attempting to map real world data onto the model.
This data from Energy Action provides Fuel consumption on several levels, including world, regional, and national. The cumulative value for World would be fed into the top level cell. 4 subcells would be created below it to contain the regions North America, Europe, Asia Pacific, and one to contain everything else. On the national level, we can again create two subcells of North America; one to represent the USA and one to hold accounting information for Canada, Mexico, and Latin America combined.
Primary Energy Consumption by Fuel
Million tonnes oil equivalent - 1999
|
Now by cross-referencing population statistics for the year 1999 from the International Energy Annual reference, we can arrive at the following rough per-capita statistics:
|
|
|
|
|
|
Population (millions) |
Total Fuel Consumption |
Per capita |
|
|
USA |
272.69 |
2204.9 |
8.0857 |
|
N Amer |
400.52 |
2557.3 |
6.3849 |
|
Europe |
863.73 |
1800.4 |
2.0844 |
|
Asia Pac. |
3,375.40 |
2255 |
0.6681 |
|
Other |
1,352.48 |
1920.7 |
1.4201 |
|
World |
5,992.13 |
8533.4 |
1.4241 |
|
|
|
|
|
Despite the wide range of per capita usage, the subpartitioning of the cell hierarchy ensures that groups of like individuals are distributed near each other, so we don't smooth too much of the complexity out of the real system. We can further use Energy Information Administration data to specify energy utilization breakdown for residential, commercial/industrial (we need not make a distinction for our purposes), and transportation uses. The reaction equations can be used to close the loop on the system and estimate how much waste products were produced that need to be dealt with.
Specifications
For Arcology Primitive Requirements
1. Attend to basic occupant needs defined in the Individual use cases described in Live.
1.1.1. Food : > 1.77 kg per diem
1.1.2. Water : > 2.3 kg per diem
1.1.3. Other consumables (vitamins, nutrients, etc.)
1.2. Indirect assets & qualities
1.2.1. Shelter, security : distribution of 5 - 10 hours of sleep, personal living quarters with > 37 m2 of personal living space.
1.2.2. Health, hygiene maintenance not covered by 1.1.3 – timely delivery of emergency supplies & services.
1.2.2.1. Waste removal – roughly equivalent to total of Provisions.
2. Self-sufficiency & sustainability
2.1. Extract required resources from environment – varies, should balance with environmental production rates, if known.
2.2. Extract labor from occupants – a distribution of around 1/3 of the daily cycle. Provide > 19 m2 of work space.
3. Improve quality of life for occupants : continually increase amount of leftover time dedicated to the following:
3.1. Education
3.2. Entertainment
3.3. Social interaction
Arcology Derived Requirements
1. Transformations of resources
1.1. Fuel to Waste – roughly 1 to 1 conversion factor by weight.
1.2. Construction / deconstruction mechanism –
2. Accounting & transportation mechanism for resources – Conversion, creation, consumption of each class of resource.
3. Transportation mechanism for resources & occupants –
3.1. Quantify measures of effectiveness – cost, latency, throughput, efficiency
Tradeoff Analysis
This simulation model will essentially be a scoring system in and of itself, as it provides output parameters that can be combined to form a composite score. Analytic Hierarchy Process would probably not be appropriately applied here, since the model produces quantitative results well suited for the scoring process, and is not so much intended to rank cities based on their performance.
The simulation system culminates in the ability to reduce piles of data into simple measures of effectiveness that can be used to compare several city designs or evaluate several potential changes to the operation of one city, and also reflect its impact on both higher levels of organization on down to the low levels of individual life.
Since most of the measures of effectiveness are ratios that range between 0 and 1, there are no concerns about recentering scores or establishing scale factors. Breaking down metrics to be expressed in this type of nondimensional form has been a longtime stalwart of supporting aerospace engineering research, where oftentimes theorists raised on entirely different unit systems could compare performance based on dimensionless parameters.
The only task remaining to form a composite score is choosing the weights to assign to each performance metric. The scoring method works best when all of the weights are normalized.
For this project, we will perform an example preliminary design tradeoff study focusing on the transportation system used to distribute goods to the population at large.
The optimization is performed using a transportation model that optimizes delivery schedules through a series of equidistant nodes. The nodes are specialized in producing a particular resource, which needs to be distributed to the other nodes that don't have that resource. A common distribution paradigm is to have a large hub that collects all of the resources, and then distributes the complete package to the destination nodes. This works well for relatively small nodes, for example, distributing goods from a city (hub) to its surrounding suburbs. However, as the relative sizes of the nodes increase to the point where adjacent nodes are peers, a different approach may be warranted.
The optimization problem used is a mixed integer / linear program that takes several input parameters characterizing the transportation network topology and demand levels, and outputs an optimal schedule of flights. We will model our demand in terms of unique resources generated at a particular node that must be distributed to all of the other nodes in the system proportional to their population. The problem was originally designed for moving passengers through the airliners, thus the passenger/aircraft terminology. However, the same model could apply just as well to moving freight through a network served by a fleet of cargo vehicles.
As a simplification, we will wrap up all of the user requirements declared in the specifications into a unit package. Therefore, every unit that makes it through the transportation network will satisfy part of the requirement for one individual in the system.
Design / Decision Variables
System Wide Measures of Effectiveness
In general, the complete city system can only improve properly if we choose the right performance metrics to judge it by. An optimization function that optimizes the wrong metric will certainly cut you short of fulfilling your goals. For a city, the metrics we would want to track include:
- Resource production / consumption ratio per cell. An effective system would need to be efficient at doing a lot with the resources it has available to consume. The emphasis should not be merely on stinginess with resources, because that can only cause stagnation.
- Transportation overhead – Establish metrics to track the ratio of resources spent on the connective infrastructure compared to the nodes and activities it actually supports. Of course, this also needs to be balanced with the need for growth and interconnectivity, so it should be considered secondary to productivity.
- Sustainability – The environment is usually the first to give resources or absorb waste when they are not serviceable elsewhere. However, it is often not well known what the capacity of the environment to perform restorative reactions on waste resources to turn them back into useful resources. The burden should be placed on the industries who exercise the environment the most to prove what its capacity is, and to achieve a suitable equilibrium.
- Quality of life – This can be measured by tracking the rate of failed reactions scheduled by the population to maintain their desired standard of living. Of course, this is dependent upon how high that initial standard is set. The only qualification for this model is to attempt to keep the quality from dropping below former levels.
Transportation System Preliminary Design Input Parameters
Define a distribution system topology. All nodes will be fully connected, but have different hub/node size ratio. What characterizes the difference between hubs and ordinary nodes? Hubs will have higher transit demand levels as well as larger throughput limitations.
Number of people per node ratio. For the same total population, is it better to have them distributed across several nodes, or occupy relatively few. This will likely be dependent on throughput limitations.
Population / number of transport vehicle ratio. For the same total population, is it better to have fewer vehicles working complex routes, or many vehicles working in parallel.
Transportation System Measures of Effectiveness for Tradeoff Analysis
The following criteria form the core of the multi-criteria optimization performed for tradeoff studies.
- Maximize profit of running the system, represented by the total freight revenues less the total cost of operating the fleet of vehicles. Revenue is generated by sending a unit of cargo to its destination. A flat cost characterizes the expenses of each segment that the cargo haulers travel. Plus, another flat cost characterizes daily maintenance expenses for having the vehicle in operation, to encourage the schedule to use fewer vehicles if possible.
- Maximize the coverage & service of the system (minimize the number of unserved people). Usually it's unprofitable to transport the last few units of cargo left at a node for the day, since they don't fill up the cargo holds enough to offset the fixed cost of the journey. Minimizing this criteria attempts to serve all of these "leftover" bits at an operating loss if necessary.
- Minimize the deviation from an arbitrary desired fleet size. A somewhat artificial metric, this criteria attempts to find a solution using a specific number of vehicles. Often, the solution would require more vehicles than you may have in operation, and you would want to avoid temporarily leasing if possible, even if it affects the other optimization criteria. On the other hand, the profit optimal solution may require less vehicles than you have in your fleet, but union labor mandates or other reasons may drive you to want to use those vehicles anyway without giving them a throwaway schedule.
Optimization Problem Formulation
A computer script in PERL generates the optimization problem and performs the multi-criteria optimization runs to populate trade study curves. The source is listed in appendix A, and an example of its output is listed in appendix B. The model is written in the LINDO-esque lp_solve model format, but is then converted to the industry-standard .mps format so just about any MIP solver can tackle it. However, the formatting of the results is tuned to accept the format of the particular MIP solver used, GNU glpk.
Pareto Optimal Solution Space
We start by optimizing for the minimum deviation from the desired fleet size. The desired fleet size is set pretty low, to 2, in order to get several points. The optimal fleet size given by optimizing most of the other metrics is 6, so by relaxing the deviation from desired fleet size constraint, we can get a feel for the pareto optimal curves.
Allowing the deviation to increase allows us to serve more customers, until all of them have been accounted for. This looks fairly linear now due to the small number of nodes and aircraft involved.
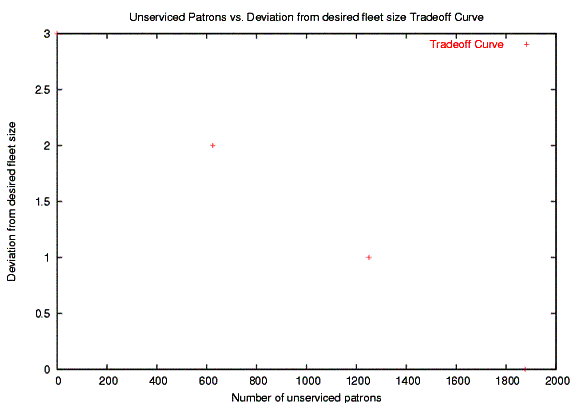
Profit also increases as we are allowed to utilize more vehicles:
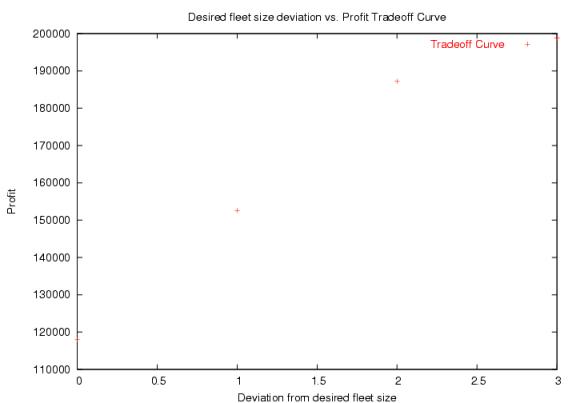
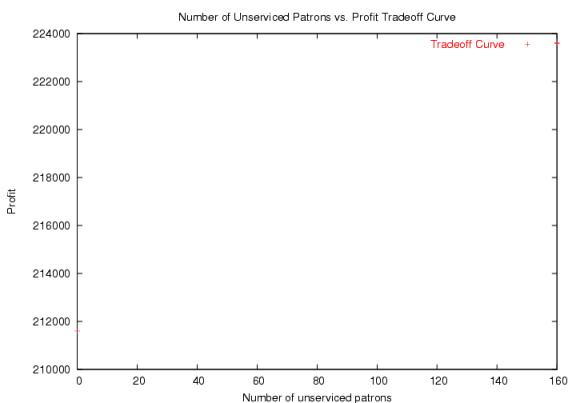
Finally, we see that we can increase profit margins by serving less people at a loss.
Preliminary System Design Solution
Bibliography & References
Soleri, Paolo; Arcology: The City in the Image of Man; Bridgewood Press 1999
Arcology.com: Architecture + Ecology
Arcosanti: A Prototype Arcology
Carfree Cities
Ilogix Rhapsody in C++
http://www.ilogix.com/products/rhapsody/rhap_incplus.cfm
Gigabyte's SimCity 2000 Arcology page
http://www.angelfire.com/hi/gigabyte2/arco.html
SimCity 3000 Plus: The First Rowan University SC3000 Site
http://users.rowan.edu/~cull2722/simcity3000.html
The Sims Online
http://www.ea.com/eagames/official/thesimsonline/home/index.jsp?
Energy Action
International Energy Annual Population Table
http://www.eia.doe.gov/emeu/iea/tableb1.html
DOA Energy Information Administration
Artemis Project: Reduction of Imported Consumables for Life Support Maintenance
http://www.asi.org/adb/04/03/05/consumable-reduction.html
Appendix
Schedgen.pl Source Listing
#!/usr/bin/perl -w
# Generate a passenger-centric LP to optimize an airline flight scedule
# Rowin Andruscavage
# ENCE 667 SP02 Dr. S. Gabriel
#
# 5/15/2003 Add input/output metrics for ENPM642 trade study
##
## Constants
##
# The traveling population
$population = 2500;
##
## Inputs
##
## hub / node ratio
$r_hub_node = 2; # range from 1.0 <= x
# number of aircraft that can arrive/leave in one timestep
# corresponds to the number of gates / loading docks
$node_maxthroughput = 3;
$hub_maxthroughput = $node_maxthroughput * $r_hub_node;
# population / number of nodes ratio
$numnodes = 4; # range from 1 < x < 100
$numhubs = 1;
$r_pop_numnodes = $population / $numnodes;
# population / number of vehicles ratio
$maxaircraft = 7;
$desirednumac = 2;
$r_pop_aircraft = $population / $maxaircraft;
$nn = $numnodes; # number of nodes (airports) in the system [0 < x < 100]
$nh = $numhubs; # number of hub nodes [0 < x < $nn]
$nt = 4; # number of time increments [1 < x < 10]
$ns = 1; # number of aircraft types [0 < x < 10]
## initial demand for travel to each node
# scale population per node relative to node size - hubs get more
# passengers proportional to hub/node ratio
$hoph2h = $nh * ($nh - 1); # hub to hub segments
$hopn2n = ($nn - $nh) * ($nn - $nh - 1); # node to node segments
$hoph2n = $nn * ($nn - 1) - $hoph2h - $hopn2n; # hub to/from node segments
## nominal ordinary none to node demand
$defdemand = $population / ( $hoph2h * $r_hub_node**2
+ $hoph2n * $r_hub_node + $hopn2n); for ($i=0; $i<$nn; $i++) {
for ($k=0; $k<$nn; $k++) { if ($i != $k) { # scale population relative to hub size ## int($x + 0.5) is a cheesy substitute for perl's lack of ## a round() function if ($i < $nh && $k < $nh) { # hub to hub $initdemand[$i][$k] = int($defdemand * $r_hub_node**2 + 0.5); } elsif ($i < $nh || $k < $nh) { # node to/from hub $initdemand[$i][$k] = int($defdemand * $r_hub_node + 0.5); } else { # node to node $initdemand[$i][$k] = int($defdemand + 0.5); } } }} ## Revenue per passenger delivered src to dest
$defsc = 200;
for ($i=0; $i<$nn; $i++) {
$sc[$i] = $defsc;} ## Runway capacity at each airport node, landings + takeoffs per timestep
for ($i=0; $i<$nn; $i++) {
if ($i<$nh) { $ncap[$i] = $hub_maxthroughput; } else { $ncap[$i] = $node_maxthroughput; }} ## parameter for each aircraft type s
# $dur = 1; # flight duration between nodes in timesteps
@fc = ( 17000, 42000 ); # Flight cost by aircraft type
@aac = ( 10000, 40000 ); # Aircraft acquisition cost by aircraft type
@fcap = ( 200, 550 ); # Max seats per flight by aircraft type
## Number of aircraft of each type (row) starting at each node (col)
#$defsupply = 3;
#for ($s=0; $s<$ns; $s++) {
# for ($i=0; $i<$nn; $i++) {
# $initsupply[$s][$i] = $defsupply;
# }
#}
## Multicriteria optimization loops
@opt_bases = ("numacdev", "numunsrv", "profit");
foreach $opt_base (@opt_bases) {
## re-sort @opt_bases array so the current entry goes first @opt_bases2 = @opt_bases; until ($opt_base eq $opt_bases2[0]) { push(@opt_bases2, shift(@opt_bases2)); ## actually, we can just get rid of half or our cases# shift(@opt_bases2);
}# print join(':', @opt_bases) . "\n";
# print join(':', @opt_bases2). "\n";
foreach $opt_subcrit (@opt_bases2) { if ($opt_subcrit eq $opt_base) { $dir = "$opt_base"; } else { $dir = "$opt_base/$opt_subcrit"; } mkdir($dir); ##
## Tweak base optimal solutions as constraints
##
## number of points to try to relax values at ## correspondes to resolution of the tradeoff curve $numpts = 8; $relax = 0; $first = 0; if (!($opt_subcrit eq $opt_base)) { $relax = 1; ## Turn on the relaxation loop $first = 1;## read the optimal value of the base optimization
%baseresults = &readresults("$opt_base/output.csv"); $basevalue = $baseresults{$opt_base}; } $value = ""; foreach (my $relx=0.0; $relx<1.0; $relx+=1.0/$numpts) { if ($relax == 1) {# profit
if ($opt_base eq "profit") { my $newvalue = $basevalue - 2 * $basevalue * $relx; if ($value == $newvalue) { unless ($first == 1) { next; # no change, skip to next $relx } } $value = $newvalue; $relaxbaseopt = "profit >= $value;\n"; } # number of unserved people
elsif ($opt_base eq "numunsrv") { my $newvalue = int($basevalue + ($population - $basevalue) * $relx + 0.5); if ($value == $newvalue) { unless ($first == 1) { next; # no change, skip to next $relx } } $value = $newvalue; $relaxbaseopt = "numunsrv <= $value; \n"; } # deviation from standard fleet size
elsif ($opt_base eq "numacdev") { my $maxdev = ($desirednumac > ($maxaircraft - $desirednumac) ? $desirednumac : $maxaircraft - $desirednumac); my $newvalue = int($basevalue + $maxdev * $relx + 0.5); if ($value == $newvalue) { unless ($first == 1) { next; # no change, skip to next $relx } } $value = $newvalue; $relaxbaseopt = "numacdev <= $value; \n"; } } ##
## LP formulation starts here
##
%input = (
population => "$population", r_hub_node => "$r_hub_node", node_maxthroughput => "$node_maxthroughput", hub_maxthroughput => "$hub_maxthroughput", numnodes => "$numnodes", numhubs => "$numhubs", r_pop_numnodes => "$r_pop_numnodes", maxaircraft => "$maxaircraft", desirednumac => "$desirednumac", r_pop_aircraft => "$r_pop_aircraft", time_incr => "$nt", defsc => "$defsc", fc => "$fc[0]", aac => "$aac[0]", fcap => "$fcap[0]", ); print "\n\n--------------------------------------------------------------
Creating lp in $dir ...\n";
open (LPM, ">$dir/sched.lpm");
##
## output metrics
##
# profit
if ($opt_subcrit eq "profit" || ($opt_base eq "profit" && $opt_subcrit eq "profit")) {
print LPM "max: profit;\n";} # number of unserved people
elsif ($opt_subcrit eq "numunsrv" || ($opt_base eq "numunsrv" && $opt_subcrit eq "numunsrv")) {
print LPM "min: numunsrv ; /* number of unserved passengers */\n";} # deviation from standard fleet size
elsif ($opt_subcrit eq "numacdev" || ($opt_base eq "numacdev" && $opt_subcrit eq "numacdev")) {
print LPM "min: numacdev; /* number of aircraft in service */\n";} ## relax base optimal value constraints if ($relax == 1) { print LPM $relaxbaseopt; } print LPM "/*
Three airports, three time increments
ptiijjkk : people from node i going to node j at time t with final destination k
ftsiijj : flights of type s from node i going to node j at time t
pptiikk : pool of people at node i at time t whose destination is node k
aptsii : pool of aircraft of type s at node i at time t
*/\n\n";
print LPM "/* Profit = passenger revenue - total flight cost
- (aircraft acquisition cost * number of aircraft)
*/
tpr - tfc - $aac[0] * numac = profit ;\n";
$t = $nt;
for ($k=1; $k<=$nn; $k++) {
&mkdd($k); print LPM "+ $sc[$k-1] pp$t$k$k ";}print LPM "- tpr = 0 ; \n\n";
print LPM "/* Total flight cost */\n";
for ($t=1; $t<=$nt; $t++) {
for ($i=1; $i<=$nn; $i++) { for ($j=1; $j<=$nn; $j++) { if ($i != $j) { for ($s=1; $s<=$ns; $s++) { &mkdd($i,$j); print LPM "+ $fc[$s-1] f$t$s$i$j "; } } } } print LPM "\n";} print LPM "- tfc = 0 ; \n\n"; print LPM "/* Initial distribution of demand */\n";
$t=0;
for ($i=1; $i<=$nn; $i++) {
for ($k=1; $k<=$nn; $k++) { if ($i != $k) { &mkdd($i,$k); # initial demand for travel from/to print LPM "pp$t$i$k = $initdemand[$i-1][$k-1] ; \n"; } else { &mkdd($k); # initial pool of passengers at their final destination print LPM "pp$t$k$k = 0 ; \n"; } }} print LPM "\n"; print LPM "/* unserved persons remaining at time = $nt */\n";
$t=$nt;
for ($i=1; $i<=$nn; $i++) {
for ($k=1; $k<=$nn; $k++) { if ($i != $k) { &mkdd($i,$k); print LPM "+ pp$t$i$k "; } ## else unconstrained final pool of passengers at their final destination }} print LPM " = numunsrv ; \n\n"; print LPM "/* initial aircraft starting positions = final positions */\n";
$t = 0;
for ($i=1; $i<=$nn; $i++) {
if ($i != $j) { for ($s=1; $s<=$ns; $s++) { &mkdd($i); print LPM "ap$t$s$i = ap$nt$s$i ; \n"; } }} print LPM "\n"; print LPM "/* max aircraft */\n";
$t=0;
for ($i=1; $i<=$nn; $i++) {
if ($i != $j) { for ($s=1; $s<=$ns; $s++) { &mkdd($i); print LPM "+ ap$t$s$i "; } }} print LPM " - numac = 0 ; numac <= $maxaircraft ;
spareacp + spareacm - numacdev = 0;
spareacp >= 0;
spareacm >= 0;
numac + spareacp - spareacm = $desirednumac;
\n\n";
print LPM "/* Apply flight capacities */\n";
for ($t=1; $t<=$nt; $t++) {
for ($i=1; $i<=$nn; $i++) { for ($j=1; $j<=$nn; $j++) { if ($i != $j) { # no flights to nowhere for ($k=1; $k<=$nn; $k++) { if ($i != $k) { # no one leaves their destination &mkdd($i,$j,$k); print LPM "+ p$t$i$j$k "; } } for ($s=1; $s<=$ns; $s++) { &mkdd($i,$j); print LPM "- $fcap[$s-1] f$t$s$i$j "; } print LPM "< 0 ; \n"; } } } print LPM "\n";} print LPM "\n"; print LPM "/* Apply airport capacities */\n";
for ($t=1; $t<=$nt; $t++) {
for ($i=1; $i<=$nn; $i++) { for ($j=1; $j<=$nn; $j++) { if ($i != $j) { # no flights to nowhere $tmo = $t - 1; for ($s=1; $s<=$ns; $s++) { &mkdd($i,$j); print LPM "+ f$t$s$i$j + f$tmo$s$j$i "; } print LPM " < $ncap[$i-1] ; \n"; } } } print LPM "\n";} print LPM "\n"; # currently assumes flight duration $dur = 1
print LPM "/* Apply aircraft movements */\n";
for ($s=1; $s<=$ns; $s++) {
for ($t=1; $t<=$nt; $t++) { for ($i=1; $i<=$nn; $i++) { for ($j=1; $j<=$nn; $j++) { if ($i != $j) { # no flights to nowhere $tmo = $t - 1; # previous timestep &mkdd($i,$j); print LPM "- f$t$s$i$j + f$tmo$s$j$i "; } } &mkdd($i); print LPM "+ ap$tmo$s$i - ap$t$s$i = 0 ; \n"; } }} print LPM "\n\n"; print LPM "/* Apply time 0 constraints - no flights */\n";
$t=0;
for ($i=1; $i<=$nn; $i++) {
for ($j=1; $j<=$nn; $j++) { if ($i != $j) { for ($s=1; $s<=$ns; $s++) { &mkdd($i,$j); print LPM "f$t$s$i$j = 0 ; \n"; } } }} print LPM "\n\n"; # Assumes $dur = 1;
print LPM "/* Apply passenger movements */\n";
for ($t=1; $t<=$nt; $t++) {
$tmo = $t - 1; # previous timestep for ($k=1; $k<=$nn; $k++) { for ($i=1; $i<=$nn; $i++) { if ($i != $k) { # no passengers leave their destination for ($j=1; $j<=$nn; $j++) { if ($j != $i) { # no passengers going nowhere # passengers leaving &mkdd($i,$j,$k); print LPM "- p$t$i$j$k "; if ($j != $k) { # no passengers leave their destination # passengers arriving &mkdd($i,$j,$k); print LPM "+ p$tmo$j$i$k "; } } } # update passenger pools &mkdd($i,$k); print LPM "+ pp$tmo$i$k - pp$t$i$k = 0 ; \n"; } else { # pool of people who arrived at their destination for ($j=1; $j<=$nn; $j++) { if ($j != $k) { # no passengers going nowhere # number of passengers arriving destination &mkdd($j,$k); print LPM "+ p$tmo$j$k$k "; } } # passenger pool who arrived at their destination &mkdd($k); print LPM "+ pp$tmo$k$k - pp$t$k$k = 0 ; \n"; } } }} print LPM "\n\n"; print LPM "/* Apply time 0 constraints - no passenger movements */\n";
$t=0;
for ($i=1; $i<=$nn; $i++) {
for ($j=1; $j<=$nn; $j++) { if ($i != $j) { # no passengers going nowhere for ($k=1; $k<=$nn; $k++) { if ($i != $k) { # no passengers leaving their destination &mkdd($i,$j,$k); print LPM "p$t$i$j$k = 0 ; \n"; } } } }} print LPM "\n\n"; print LPM "/* Apply integer constraint to flights */\n";
print LPM "int ";
for ($t=1; $t<=$nt; $t++) {
for ($i=1; $i<=$nn; $i++) { for ($j=1; $j<=$nn; $j++) { if ($i != $j) { for ($s=1; $s<=$ns; $s++) { &mkdd($i,$j); print LPM "f$t$s$i$j"; unless (($t==$nt) && ($i==$nn) && ($j==$nn-1) && ($s==$ns)) { print LPM " , "; } } } } }} print LPM " ;\n\n"; close (LPM);
##
## End of LP formulation
##
## DEBUG
# if( 0 ) {
print "Solving LP ...\n";
system("lp2mps < $dir/sched.lpm > $dir/sched.mps; glpsol -o $dir/sched.ogl $dir/sched.mps");
## Make a human-readable results summary for debugging
system("
echo \"Results\" > $dir/results.txt
grep profit $dir/sched.ogl >> $dir/results.txt
grep tfc $dir/sched.ogl >> $dir/results.txt
grep tpr $dir/sched.ogl >> $dir/results.txt
grep numac $dir/sched.ogl >> $dir/results.txt
grep numunsrv $dir/sched.ogl >> $dir/results.txt
echo \"Flight schedule:\" >> $dir/results.txt
grep f[0-9] $dir/sched.ogl | grep \" [1-9] \" | sort -k 2 >> $dir/results.txt
echo \"Passenger pools\" >> $dir/results.txt
grep pp[0-9] $dir/sched.ogl | sort -k 2 >> $dir/results.txt
echo \"Aircraft pools\" >> $dir/results.txt
grep ap[0-9] $dir/sched.ogl | grep \" [1-9] \" | sort -k 2 >> $dir/results.txt
");
print "Reading results ... \n";
open(RESULTS, "$dir/sched.ogl");
@rawresults = <RESULTS>;
close(RESULTS);
@results = (grep(/profit/, @rawresults),
grep(/tfc/, @rawresults), grep(/tpr/, @rawresults), grep(/numac/, @rawresults), grep(/numacdev/, @rawresults), grep(/numunsrv/, @rawresults));# print join("\n", @results);
%output = ();
foreach $line (@results) {
@field = split(/\s+/,$line);# print join(':', @field) . "\n";
$output{$field[2]} = $field[3];} if ($relax == 0 || ($relax == 1 && $first == 1)) { open (OUTPUT, ">$dir/output.csv"); ## print line of column numbers print OUTPUT "#"; my $xiter = 0; foreach $key (keys %input) { $xiter++; print OUTPUT "$xiter,"; } foreach $key (keys %output) { $xiter++; print OUTPUT "$xiter,"; } print OUTPUT "\n"; ## print line of keys print OUTPUT "#"; foreach $key (keys %input) { print OUTPUT "$key,"; } foreach $key (keys %output) { print OUTPUT "$key,"; } if ($relax == 1) { chomp $relaxbaseopt; print OUTPUT $relaxbaseopt; } print OUTPUT "\n"; close (OUTPUT); } open (OUTPUT, ">>$dir/output.csv"); foreach $key (keys %input) { print OUTPUT "$input{$key},"; } foreach $key (keys %output) { print OUTPUT "$output{$key},"; } if ($relax == 1) { $first = 0; ## not first relax loop anymore ## record how this line was constrained print OUTPUT "$value"; } ## no trailing comma print OUTPUT "\n"; close (OUTPUT); ## only loop through once if not playing with relaxed constraints
unless ($relax == 1) { last; } } # foreach $relx } # foreach $opt_subcrit} # foreach $opt_base #} ## DEBUG
## change numeric vars to double digit format
sub mkdd {
foreach (@_) { if ($_ > 99) { print STDERR "Overflow: $_ over double digits!\n"; exit; } $_ = sprintf("%02d", $_); } return @_;} ## Reads first two lines of a csv file (name given in $_[0]) and
## returns a hash of its keys => values
sub readresults {
open (BASERESULTS, $_[0]); my @baseresults = <BASERESULTS>; close (BASERESULTS); ## skip first line are just column numbers my @bkeys = split(/,/, $baseresults[1]); my @bvals = split(/,/, $baseresults[2]); my %baseresults = (); for (my $x=0; $x<$#bkeys; $x++) { $baseresults{$bkeys[$x]} = $bvals[$x]; } return %baseresults;}
Example Mixed Integer Programming Model
max: profit;
numacdev <= 4; /*
Three airports, three time increments
ptiijjkk : people from node i going to node j at time t with final destination k
ftsiijj : flights of type s from node i going to node j at time t
pptiikk : pool of people at node i at time t whose destination is node k
aptsii : pool of aircraft of type s at node i at time t
*/
/* Profit = passenger revenue - total flight cost
- (aircraft acquisition cost * number of aircraft)
*/
tpr - tfc - 10000 * numac = profit ;+ 200 pp40101 + 200 pp40202 + 200 pp40303 + 200 pp40404 - tpr = 0 ; /* Total flight cost */
+ 17000 f110102 + 17000 f110103 + 17000 f110104 + 17000 f110201 + 17000 f110203 + 17000 f110204 + 17000 f110301 + 17000 f110302 + 17000 f110304 + 17000 f110401 + 17000 f110402 + 17000 f110403+ 17000 f210102 + 17000 f210103 + 17000 f210104 + 17000 f210201 + 17000 f210203 + 17000 f210204 + 17000 f210301 + 17000 f210302 + 17000 f210304 + 17000 f210401 + 17000 f210402 + 17000 f210403+ 17000 f310102 + 17000 f310103 + 17000 f310104 + 17000 f310201 + 17000 f310203 + 17000 f310204 + 17000 f310301 + 17000 f310302 + 17000 f310304 + 17000 f310401 + 17000 f310402 + 17000 f310403+ 17000 f410102 + 17000 f410103 + 17000 f410104 + 17000 f410201 + 17000 f410203 + 17000 f410204 + 17000 f410301 + 17000 f410302 + 17000 f410304 + 17000 f410401 + 17000 f410402 + 17000 f410403- tfc = 0 ; /* Initial distribution of demand */
pp00101 = 0 ;pp00102 = 278 ;pp00103 = 278 ;pp00104 = 278 ;pp00201 = 278 ;pp00202 = 0 ;pp00203 = 139 ;pp00204 = 139 ;pp00301 = 278 ;pp00302 = 139 ;pp00303 = 0 ;pp00304 = 139 ;pp00401 = 278 ;pp00402 = 139 ;pp00403 = 139 ;pp00404 = 0 ; /* unserved persons remaining at time = 4 */
+ pp40102 + pp40103 + pp40104 + pp40201 + pp40203 + pp40204 + pp40301 + pp40302 + pp40304 + pp40401 + pp40402 + pp40403 = numunsrv ; /* initial aircraft starting positions = final positions */
ap0101 = ap4101 ;ap0102 = ap4102 ;ap0103 = ap4103 ;ap0104 = ap4104 ; /* max aircraft */
+ ap0101 + ap0102 + ap0103 + ap0104 - numac = 0 ;numac <= 7 ;spareacp + spareacm - numacdev = 0;spareacp >= 0;spareacm >= 0;numac + spareacp - spareacm = 2; /* Apply flight capacities */
+ p1010202 + p1010203 + p1010204 - 200 f110102 < 0 ;+ p1010302 + p1010303 + p1010304 - 200 f110103 < 0 ;+ p1010402 + p1010403 + p1010404 - 200 f110104 < 0 ;+ p1020101 + p1020103 + p1020104 - 200 f110201 < 0 ;+ p1020301 + p1020303 + p1020304 - 200 f110203 < 0 ;+ p1020401 + p1020403 + p1020404 - 200 f110204 < 0 ;+ p1030101 + p1030102 + p1030104 - 200 f110301 < 0 ;+ p1030201 + p1030202 + p1030204 - 200 f110302 < 0 ;+ p1030401 + p1030402 + p1030404 - 200 f110304 < 0 ;+ p1040101 + p1040102 + p1040103 - 200 f110401 < 0 ;+ p1040201 + p1040202 + p1040203 - 200 f110402 < 0 ;+ p1040301 + p1040302 + p1040303 - 200 f110403 < 0 ; + p2010202 + p2010203 + p2010204 - 200 f210102 < 0 ;+ p2010302 + p2010303 + p2010304 - 200 f210103 < 0 ;+ p2010402 + p2010403 + p2010404 - 200 f210104 < 0 ;+ p2020101 + p2020103 + p2020104 - 200 f210201 < 0 ;+ p2020301 + p2020303 + p2020304 - 200 f210203 < 0 ;+ p2020401 + p2020403 + p2020404 - 200 f210204 < 0 ;+ p2030101 + p2030102 + p2030104 - 200 f210301 < 0 ;+ p2030201 + p2030202 + p2030204 - 200 f210302 < 0 ;+ p2030401 + p2030402 + p2030404 - 200 f210304 < 0 ;+ p2040101 + p2040102 + p2040103 - 200 f210401 < 0 ;+ p2040201 + p2040202 + p2040203 - 200 f210402 < 0 ;+ p2040301 + p2040302 + p2040303 - 200 f210403 < 0 ; + p3010202 + p3010203 + p3010204 - 200 f310102 < 0 ;+ p3010302 + p3010303 + p3010304 - 200 f310103 < 0 ;+ p3010402 + p3010403 + p3010404 - 200 f310104 < 0 ;+ p3020101 + p3020103 + p3020104 - 200 f310201 < 0 ;+ p3020301 + p3020303 + p3020304 - 200 f310203 < 0 ;+ p3020401 + p3020403 + p3020404 - 200 f310204 < 0 ;+ p3030101 + p3030102 + p3030104 - 200 f310301 < 0 ;+ p3030201 + p3030202 + p3030204 - 200 f310302 < 0 ;+ p3030401 + p3030402 + p3030404 - 200 f310304 < 0 ;+ p3040101 + p3040102 + p3040103 - 200 f310401 < 0 ;+ p3040201 + p3040202 + p3040203 - 200 f310402 < 0 ;+ p3040301 + p3040302 + p3040303 - 200 f310403 < 0 ; + p4010202 + p4010203 + p4010204 - 200 f410102 < 0 ;+ p4010302 + p4010303 + p4010304 - 200 f410103 < 0 ;+ p4010402 + p4010403 + p4010404 - 200 f410104 < 0 ;+ p4020101 + p4020103 + p4020104 - 200 f410201 < 0 ;+ p4020301 + p4020303 + p4020304 - 200 f410203 < 0 ;+ p4020401 + p4020403 + p4020404 - 200 f410204 < 0 ;+ p4030101 + p4030102 + p4030104 - 200 f410301 < 0 ;+ p4030201 + p4030202 + p4030204 - 200 f410302 < 0 ;+ p4030401 + p4030402 + p4030404 - 200 f410304 < 0 ;+ p4040101 + p4040102 + p4040103 - 200 f410401 < 0 ;+ p4040201 + p4040202 + p4040203 - 200 f410402 < 0 ;+ p4040301 + p4040302 + p4040303 - 200 f410403 < 0 ; /* Apply airport capacities */
+ f110102 + f010201 < 6 ;+ f110103 + f010301 < 6 ;+ f110104 + f010401 < 6 ;+ f110201 + f010102 < 3 ;+ f110203 + f010302 < 3 ;+ f110204 + f010402 < 3 ;+ f110301 + f010103 < 3 ;+ f110302 + f010203 < 3 ;+ f110304 + f010403 < 3 ;+ f110401 + f010104 < 3 ;+ f110402 + f010204 < 3 ;+ f110403 + f010304 < 3 ; + f210102 + f110201 < 6 ;+ f210103 + f110301 < 6 ;+ f210104 + f110401 < 6 ;+ f210201 + f110102 < 3 ;+ f210203 + f110302 < 3 ;+ f210204 + f110402 < 3 ;+ f210301 + f110103 < 3 ;+ f210302 + f110203 < 3 ;+ f210304 + f110403 < 3 ;+ f210401 + f110104 < 3 ;+ f210402 + f110204 < 3 ;+ f210403 + f110304 < 3 ; + f310102 + f210201 < 6 ;+ f310103 + f210301 < 6 ;+ f310104 + f210401 < 6 ;+ f310201 + f210102 < 3 ;+ f310203 + f210302 < 3 ;+ f310204 + f210402 < 3 ;+ f310301 + f210103 < 3 ;+ f310302 + f210203 < 3 ;+ f310304 + f210403 < 3 ;+ f310401 + f210104 < 3 ;+ f310402 + f210204 < 3 ;+ f310403 + f210304 < 3 ; + f410102 + f310201 < 6 ;+ f410103 + f310301 < 6 ;+ f410104 + f310401 < 6 ;+ f410201 + f310102 < 3 ;+ f410203 + f310302 < 3 ;+ f410204 + f310402 < 3 ;+ f410301 + f310103 < 3 ;+ f410302 + f310203 < 3 ;+ f410304 + f310403 < 3 ;+ f410401 + f310104 < 3 ;+ f410402 + f310204 < 3 ;+ f410403 + f310304 < 3 ; /* Apply aircraft movements */
- f110102 + f010201 - f110103 + f010301 - f110104 + f010401 + ap0101 - ap1101 = 0 ;- f110201 + f010102 - f110203 + f010302 - f110204 + f010402 + ap0102 - ap1102 = 0 ;- f110301 + f010103 - f110302 + f010203 - f110304 + f010403 + ap0103 - ap1103 = 0 ;- f110401 + f010104 - f110402 + f010204 - f110403 + f010304 + ap0104 - ap1104 = 0 ;- f210102 + f110201 - f210103 + f110301 - f210104 + f110401 + ap1101 - ap2101 = 0 ;- f210201 + f110102 - f210203 + f110302 - f210204 + f110402 + ap1102 - ap2102 = 0 ;- f210301 + f110103 - f210302 + f110203 - f210304 + f110403 + ap1103 - ap2103 = 0 ;- f210401 + f110104 - f210402 + f110204 - f210403 + f110304 + ap1104 - ap2104 = 0 ;- f310102 + f210201 - f310103 + f210301 - f310104 + f210401 + ap2101 - ap3101 = 0 ;- f310201 + f210102 - f310203 + f210302 - f310204 + f210402 + ap2102 - ap3102 = 0 ;- f310301 + f210103 - f310302 + f210203 - f310304 + f210403 + ap2103 - ap3103 = 0 ;- f310401 + f210104 - f310402 + f210204 - f310403 + f210304 + ap2104 - ap3104 = 0 ;- f410102 + f310201 - f410103 + f310301 - f410104 + f310401 + ap3101 - ap4101 = 0 ;- f410201 + f310102 - f410203 + f310302 - f410204 + f310402 + ap3102 - ap4102 = 0 ;- f410301 + f310103 - f410302 + f310203 - f410304 + f310403 + ap3103 - ap4103 = 0 ;- f410401 + f310104 - f410402 + f310204 - f410403 + f310304 + ap3104 - ap4104 = 0 ; /* Apply time 0 constraints - no flights */
f010102 = 0 ;f010103 = 0 ;f010104 = 0 ;f010201 = 0 ;f010203 = 0 ;f010204 = 0 ;f010301 = 0 ;f010302 = 0 ;f010304 = 0 ;f010401 = 0 ;f010402 = 0 ;f010403 = 0 ; /* Apply passenger movements */
+ p0020101 + p0030101 + p0040101 + pp00101 - pp10101 = 0 ;- p1020101 - p1020301 + p0030201 - p1020401 + p0040201 + pp00201 - pp10201 = 0 ;- p1030101 - p1030201 + p0020301 - p1030401 + p0040301 + pp00301 - pp10301 = 0 ;- p1040101 - p1040201 + p0020401 - p1040301 + p0030401 + pp00401 - pp10401 = 0 ;- p1010202 - p1010302 + p0030102 - p1010402 + p0040102 + pp00102 - pp10102 = 0 ;+ p0010202 + p0030202 + p0040202 + pp00202 - pp10202 = 0 ;- p1030102 + p0010302 - p1030202 - p1030402 + p0040302 + pp00302 - pp10302 = 0 ;- p1040102 + p0010402 - p1040202 - p1040302 + p0030402 + pp00402 - pp10402 = 0 ;- p1010203 + p0020103 - p1010303 - p1010403 + p0040103 + pp00103 - pp10103 = 0 ;- p1020103 + p0010203 - p1020303 - p1020403 + p0040203 + pp00203 - pp10203 = 0 ;+ p0010303 + p0020303 + p0040303 + pp00303 - pp10303 = 0 ;- p1040103 + p0010403 - p1040203 + p0020403 - p1040303 + pp00403 - pp10403 = 0 ;- p1010204 + p0020104 - p1010304 + p0030104 - p1010404 + pp00104 - pp10104 = 0 ;- p1020104 + p0010204 - p1020304 + p0030204 - p1020404 + pp00204 - pp10204 = 0 ;- p1030104 + p0010304 - p1030204 + p0020304 - p1030404 + pp00304 - pp10304 = 0 ;+ p0010404 + p0020404 + p0030404 + pp00404 - pp10404 = 0 ;+ p1020101 + p1030101 + p1040101 + pp10101 - pp20101 = 0 ;- p2020101 - p2020301 + p1030201 - p2020401 + p1040201 + pp10201 - pp20201 = 0 ;- p2030101 - p2030201 + p1020301 - p2030401 + p1040301 + pp10301 - pp20301 = 0 ;- p2040101 - p2040201 + p1020401 - p2040301 + p1030401 + pp10401 - pp20401 = 0 ;- p2010202 - p2010302 + p1030102 - p2010402 + p1040102 + pp10102 - pp20102 = 0 ;+ p1010202 + p1030202 + p1040202 + pp10202 - pp20202 = 0 ;- p2030102 + p1010302 - p2030202 - p2030402 + p1040302 + pp10302 - pp20302 = 0 ;- p2040102 + p1010402 - p2040202 - p2040302 + p1030402 + pp10402 - pp20402 = 0 ;- p2010203 + p1020103 - p2010303 - p2010403 + p1040103 + pp10103 - pp20103 = 0 ;- p2020103 + p1010203 - p2020303 - p2020403 + p1040203 + pp10203 - pp20203 = 0 ;+ p1010303 + p1020303 + p1040303 + pp10303 - pp20303 = 0 ;- p2040103 + p1010403 - p2040203 + p1020403 - p2040303 + pp10403 - pp20403 = 0 ;- p2010204 + p1020104 - p2010304 + p1030104 - p2010404 + pp10104 - pp20104 = 0 ;- p2020104 + p1010204 - p2020304 + p1030204 - p2020404 + pp10204 - pp20204 = 0 ;- p2030104 + p1010304 - p2030204 + p1020304 - p2030404 + pp10304 - pp20304 = 0 ;+ p1010404 + p1020404 + p1030404 + pp10404 - pp20404 = 0 ;+ p2020101 + p2030101 + p2040101 + pp20101 - pp30101 = 0 ;- p3020101 - p3020301 + p2030201 - p3020401 + p2040201 + pp20201 - pp30201 = 0 ;- p3030101 - p3030201 + p2020301 - p3030401 + p2040301 + pp20301 - pp30301 = 0 ;- p3040101 - p3040201 + p2020401 - p3040301 + p2030401 + pp20401 - pp30401 = 0 ;- p3010202 - p3010302 + p2030102 - p3010402 + p2040102 + pp20102 - pp30102 = 0 ;+ p2010202 + p2030202 + p2040202 + pp20202 - pp30202 = 0 ;- p3030102 + p2010302 - p3030202 - p3030402 + p2040302 + pp20302 - pp30302 = 0 ;- p3040102 + p2010402 - p3040202 - p3040302 + p2030402 + pp20402 - pp30402 = 0 ;- p3010203 + p2020103 - p3010303 - p3010403 + p2040103 + pp20103 - pp30103 = 0 ;- p3020103 + p2010203 - p3020303 - p3020403 + p2040203 + pp20203 - pp30203 = 0 ;+ p2010303 + p2020303 + p2040303 + pp20303 - pp30303 = 0 ;- p3040103 + p2010403 - p3040203 + p2020403 - p3040303 + pp20403 - pp30403 = 0 ;- p3010204 + p2020104 - p3010304 + p2030104 - p3010404 + pp20104 - pp30104 = 0 ;- p3020104 + p2010204 - p3020304 + p2030204 - p3020404 + pp20204 - pp30204 = 0 ;- p3030104 + p2010304 - p3030204 + p2020304 - p3030404 + pp20304 - pp30304 = 0 ;+ p2010404 + p2020404 + p2030404 + pp20404 - pp30404 = 0 ;+ p3020101 + p3030101 + p3040101 + pp30101 - pp40101 = 0 ;- p4020101 - p4020301 + p3030201 - p4020401 + p3040201 + pp30201 - pp40201 = 0 ;- p4030101 - p4030201 + p3020301 - p4030401 + p3040301 + pp30301 - pp40301 = 0 ;- p4040101 - p4040201 + p3020401 - p4040301 + p3030401 + pp30401 - pp40401 = 0 ;- p4010202 - p4010302 + p3030102 - p4010402 + p3040102 + pp30102 - pp40102 = 0 ;+ p3010202 + p3030202 + p3040202 + pp30202 - pp40202 = 0 ;- p4030102 + p3010302 - p4030202 - p4030402 + p3040302 + pp30302 - pp40302 = 0 ;- p4040102 + p3010402 - p4040202 - p4040302 + p3030402 + pp30402 - pp40402 = 0 ;- p4010203 + p3020103 - p4010303 - p4010403 + p3040103 + pp30103 - pp40103 = 0 ;- p4020103 + p3010203 - p4020303 - p4020403 + p3040203 + pp30203 - pp40203 = 0 ;+ p3010303 + p3020303 + p3040303 + pp30303 - pp40303 = 0 ;- p4040103 + p3010403 - p4040203 + p3020403 - p4040303 + pp30403 - pp40403 = 0 ;- p4010204 + p3020104 - p4010304 + p3030104 - p4010404 + pp30104 - pp40104 = 0 ;- p4020104 + p3010204 - p4020304 + p3030204 - p4020404 + pp30204 - pp40204 = 0 ;- p4030104 + p3010304 - p4030204 + p3020304 - p4030404 + pp30304 - pp40304 = 0 ;+ p3010404 + p3020404 + p3030404 + pp30404 - pp40404 = 0 ; /* Apply time 0 constraints - no passenger movements */
p0010202 = 0 ;p0010203 = 0 ;p0010204 = 0 ;p0010302 = 0 ;p0010303 = 0 ;p0010304 = 0 ;p0010402 = 0 ;p0010403 = 0 ;p0010404 = 0 ;p0020101 = 0 ;p0020103 = 0 ;p0020104 = 0 ;p0020301 = 0 ;p0020303 = 0 ;p0020304 = 0 ;p0020401 = 0 ;p0020403 = 0 ;p0020404 = 0 ;p0030101 = 0 ;p0030102 = 0 ;p0030104 = 0 ;p0030201 = 0 ;p0030202 = 0 ;p0030204 = 0 ;p0030401 = 0 ;p0030402 = 0 ;p0030404 = 0 ;p0040101 = 0 ;p0040102 = 0 ;p0040103 = 0 ;p0040201 = 0 ;p0040202 = 0 ;p0040203 = 0 ;p0040301 = 0 ;p0040302 = 0 ;p0040303 = 0 ; /* Apply integer constraint to flights */
int f110102 , f110103 , f110104 , f110201 , f110203 , f110204 , f110301 , f110302 , f110304 , f110401 , f110402 , f110403 , f210102 , f210103 , f210104 , f210201 , f210203 , f210204 , f210301 , f210302 , f210304 , f210401 , f210402 , f210403 , f310102 , f310103 , f310104 , f310201 , f310203 , f310204 , f310301 , f310302 , f310304 , f310401 , f310402 , f310403 , f410102 , f410103 , f410104 , f410201 , f410203 , f410204 , f410301 , f410302 , f410304 , f410401 , f410402 , f410403 ;